车辆坐标转换

解决问题：
1）地球是不规则的球体，两极扁，赤道鼓。不能 简单地做为圆球体来计算；
2）每纬度在地理位置上的距离是一致的（约 111 km），但是每经度之间的距离是不同的（越往两极，东 西方向上的距离就越小），不能直接转换为直角坐标系；

WGS84坐标系全称World Geodetic System - 1984，是为了解决GPS定位而产生的全球统一的一个地心坐标系。
● 椭球体：WGS84椭球
● 长半径\(a=6378137m\)
● 短半径\(b=6356752.3142m\)
● 第一偏心率平方\({e_1}^2=0.00669437999013\)
● 第二偏心率平方\({e_2}^2=0.006739496742227\)
● 扁率\(\alpha=1/298.257223563\)

public static CenterCoordinate createCenterCoordinateFromBLH(double latitude, double longitude, double altitude) {
    double B = Math.toRadians(latitude);
    double L = Math.toRadians(longitude);
    double N = r/Math.sqrt(1-e*e*Math.sin(B)*Math.sin(B));
    double x = (N+altitude)*Math.cos(B)*Math.cos(L);
    double y = (N+altitude)*Math.cos(B)*Math.sin(L);
    double z = (N*(1-e*e)+altitude)*Math.sin(B);
    return new CenterCoordinate(x,y,z);
}

车辆方向转换

上面将经纬度转换为了地心直角坐标，然而速度方向拿到则是一个大陆坐标系下的与正北方的顺时针夹角。所以这里要对其进行转换。

坐标系转化

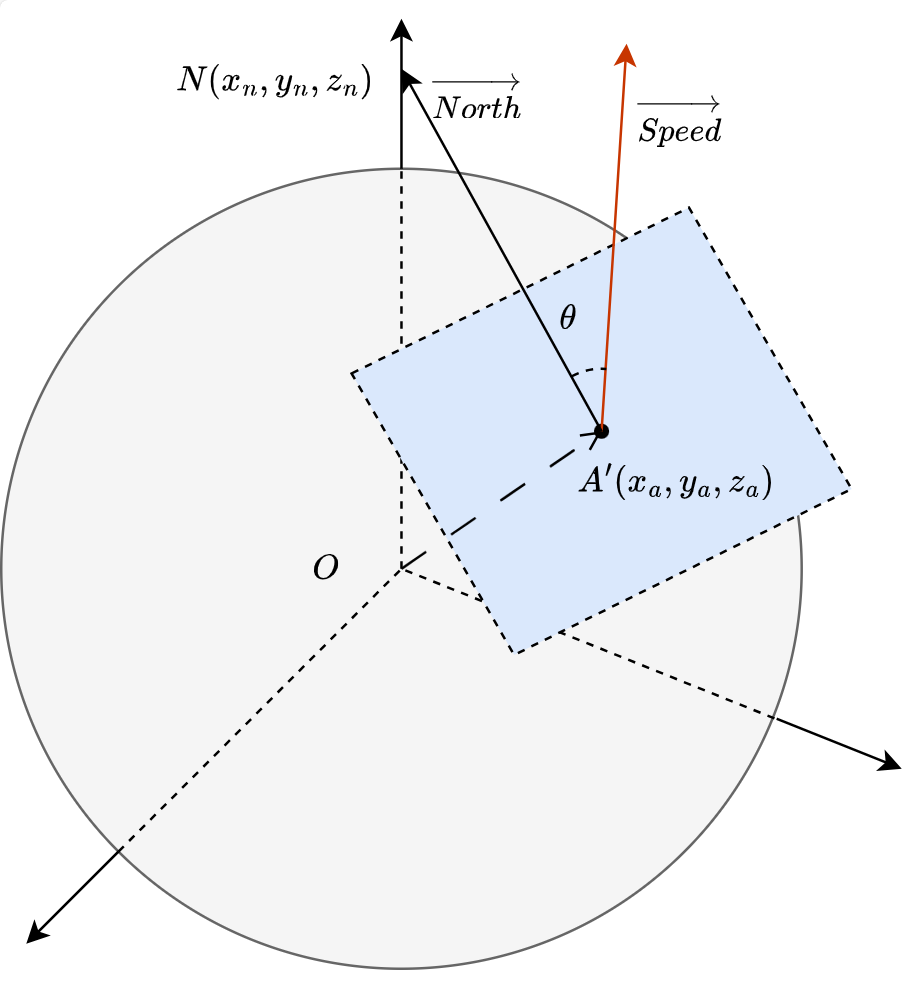
假设条件：

1. 车辆所处大陆平面坐标系与地球球面相切

已知条件为：

1. 车辆坐标 \((x_a,y_a,z_a)\)
2. 车辆速度方向与正北方顺时针夹角 \(\theta\)

首先，根据已知条件1可得车辆所属的平面的一个法向量和平面点法式方程如下： \[ \overrightarrow{OA} = \begin{bmatrix} x_a \\ y_a \\ z_a \end{bmatrix} \] \[ x_a(x-x_a) + y_a(y-y_a) + z_a(z-z_a) = 0 \]

根据假设条件1可知，平面内向北的向量 \(\overrightarrow{O'N}\)这里令其为 \(\overrightarrow{North}\)与坐标下的Z轴交于 N 点。
首先根据向量加法得到： \[ \overrightarrow{ON} = \overrightarrow{OO'} + \overrightarrow{O‘N} \]

把上式与平面方程联立可得： \[ \overrightarrow{North} = \begin{bmatrix} -x_a \\ -y_a \\ \frac{x_a^2+{y_a}^2}{z_a} \end{bmatrix} \]

根据已知条件\(\overrightarrow{Speed}\)为车辆速度的单位向量所以有： \[ \vert \overrightarrow{Speed} \vert = 1 \]

根据向量点乘公式： \[ \overrightarrow{North} \cdot \overrightarrow{Speed} = \vert \overrightarrow{North} \vert \vert \overrightarrow{Speed} \vert \cos{\theta} \]

向量 \(\overrightarrow{Speed}\)在平面上，则其与平面法向量垂直： \[ \overrightarrow{OA} \cdot \overrightarrow{Speed} = 0 \]

联立上述三个公式得到向量 \(\overrightarrow{Speed}\)表达式如下：
辅助符号： \[ D_{xy} = {x_{a}}^2+{y_{a}}^2 \] \[ D_{xyz} = {x_{a}}^2+{y_{a}}^2+{z_{a}}^2 \] \[ V = \sqrt{\frac{1-\cos^2{\theta}}{D_{xy}}} \] \[ U = \sqrt{ \frac{D_{xy} D_{xyz}}{z_a^2} } \]

解1： \[ \overrightarrow{Speed_1} = \begin{bmatrix} yV - \frac{x_{a} z_{a}^2 U\cos{\theta}}{D_{xy} D_{xyz}} \\ -xV - \frac{y z^2 U \cos{\theta}}{D_{xy} D_{xyz}} \\ \frac{z_{a} U \cos{\theta}}{D_{xyz}} \end{bmatrix} \] 解2： \[ \overrightarrow{Speed_2} = \begin{bmatrix} -yV - \frac{x_{a} z_{a}^2 U\cos{\theta}}{D_{xy} D_{xyz}} \\ xV - \frac{y z^2 U \cos{\theta}}{D_{xy} D_{xyz}} \\ \frac{z_{a} U \cos{\theta}}{D_{xyz}} \end{bmatrix} \] 当 \(\theta \in (0, \pi)\)时，取解2；当 \(\theta \in (\pi, 2 \pi)\)时，取解1；